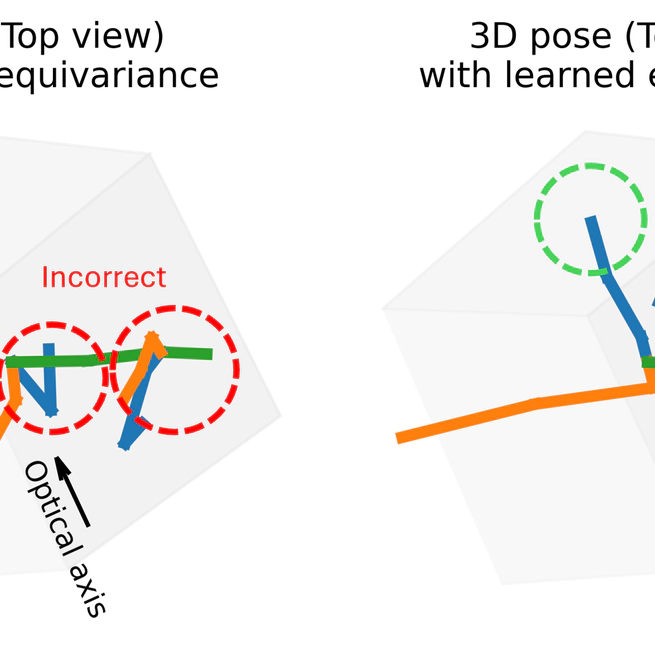
Estimating 3D from 2D is one of the central tasks in computer vision. In this work, we consider the monocular setting, i.e. single-view input, for 3D human pose estimation (HPE). Here, the task is to predict a 3D point set of human skeletal joints from a single 2D input image. While by definition this is an ill-posed problem, recent work has presented methods that solve it with up to several-centimetre error. Typically, these methods employ a two-step approach, where the first step is to detect the 2D skeletal joints in the input image, followed by the step of 2D-to-3D lifting. We find that common lifting models fail when encountering a rotated input. We argue that learning a single human pose along with its in-plane rotations is considerably easier and more geometrically grounded than directly learning a point-to-point mapping. Furthermore, our intuition is that endowing the model with the notion of rotation equivariance without explicitly constraining its parameter space should lead to a more straightforward learning process than one with equivariance by design. Utilising the common HPE benchmarks, we confirm that the 2D rotation equivariance per se improves the model performance on human poses akin to rotations in the image plane, and can be efficiently and straightforwardly learned by augmentation, outperforming state-of-the-art equivariant-by-design methods.
Jan 20, 2026
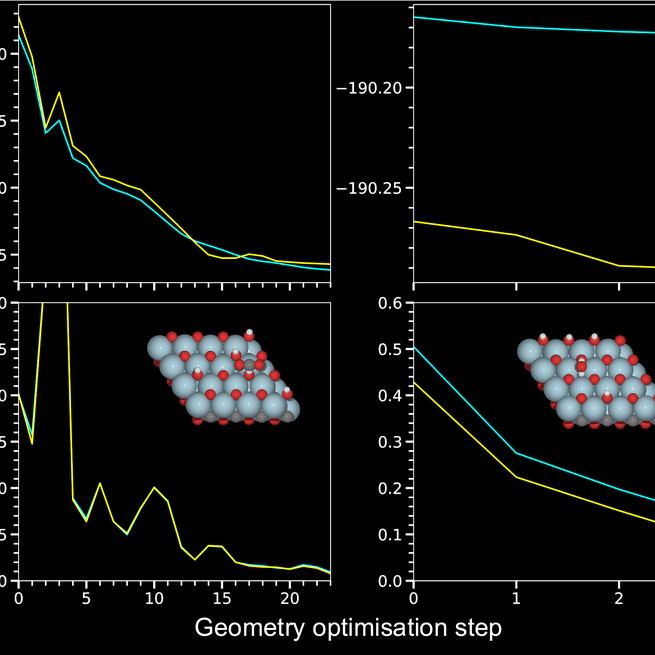
Merging advanced computations with machine learning, we aim to accelerate the exploration of catalytic behaviour in novel materials. We focus on two-dimensional (2D) Ti$_2$CT$_y$ MXenes, whose versatile surface chemistry makes them particularly compelling candidates for catalysis. However, resolving their composition and structure under realistic conditions requires going beyond the systems typically studied with density functional theory (DFT), as the computational cost of such calculations limits accessible system sizes and timescales, calling instead for more efficient approaches. To address this challenge, we generate a comprehensive dataset of 50,000 DFT calculations for training and 10,000 for testing, encompassing both Ti$_2$CT$_y$ MXene configurations and molecular systems, along with an augmented dataset where systems are artificially repeated to investigate how well models generalise to larger systems.Employing advances in geometric deep learning, we train and validate an equivariant (\ie symmetry-aware) model (EquiformerV2) that accurately predicts atomic forces and formation energies — quantities that DFT must repeatedly compute for structural and catalytic investigations — for these 2D materials. This combined DFT–ML framework achieves computational acceleration of the order ${\sim}10^3$–$10^4$ (on a CPU) while maintaining DFT-level accuracy (${\sim} {\pm} 45$ meV/Å for forces and ${\sim} {\pm} 6$ meV for per-atom energies), paving the way for more efficient investigations of MXene catalytic behaviour. Moreover, we confirm that the total energy prediction error of the model grows linearly with the number of atoms in an input system, while the force error remains the same, which, along with the equivariant model design, is a necessity for a robust model. The dataset and the trained models with the code are available at \url{https://github.com/CataLiUst}.
Nov 24, 2025

Felix Klein’s Erlangen Programme of 1872 introduced a methodology to unify non-Euclidean geometries. Similarly, geometric deep learning (GDL) constitutes a unifying framework for various neural network architectures. GDL is built from the first principles of geometry—symmetry and scale separation—and enables tractable learning in high dimensions. Symmetries play a vital role in preserving structural information of geometric data and allow models (i.e., neural networks) to adjust to different geometric transformations.\n\nIn this context, spheres exhibit a maximal set of symmetries compared to other geometric entities in Euclidean space. The orthogonal group O(n) fully encapsulates the symmetry structure of an nD sphere, including both rotational and reflection symmetries. In this thesis, we focus on integrating these symmetries into a model as an inductive bias, which is a crucial requirement for addressing problems in 3D vision as well as in natural sciences and their related applications.\n\nIn Paper A, we focus on 3D geometry and use the symmetries of spheres as geometric entities to construct neurons with spherical decision surfaces—spherical neurons—using a conformal embedding of Euclidean space. We also demonstrate that spherical neuron activations are non-linear due to the inherent non-linearity of the input embedding, and thus, do not necessarily require an activation function. In addition, we show graphically, theoretically, and experimentally that spherical neuron activations are isometries in Euclidean space, which is a prerequisite for the equivariance contributions of our subsequent work.\n\nIn Paper B, we closely examine the isometry property of the spherical neurons in the context of equivariance under 3D rotations (i.e., SO(3)-equivariance). Focusing on 3D in this work and based on a minimal set of four spherical neurons (one learned spherical decision surface and three copies), the centers of which are rotated into the corresponding vertices of a regular tetrahedron, we construct a spherical filter bank. We call it a steerable 3D spherical neuron because, as we verify later, it constitutes a steerable filter. Finally, we derive a 3D steerability constraint for a spherical neuron (i.e., a single spherical decision surface).\n\nIn Paper C, we present a learnable point-cloud descriptor invariant under 3D rotations and reflections, i.e., the O(3) actions, utilizing the steerable 3D spherical neurons we introduced previously, as well as vector neurons from related work. Specifically, we propose an embedding of the 3D steerable neurons into 4D vector neurons, which leverages end-to-end training of the model. The resulting model, termed TetraSphere, sets a new state-of-the-art performance classifying randomly rotated real-world object scans. Thus, our results reveal the practical value of steerable 3D spherical neurons for learning in 3D Euclidean space.\n\nIn Paper D, we generalize to nD the concepts we previously established in 3D, and propose O(n)-equivariant neurons with spherical decision surfaces, which we call Deep Equivariant Hyper-spheres. We demonstrate how to combine them in a network that directly operates on the basis of the input points and propose an invariant operator based on the relation between two points and a sphere, which as we show, turns out to be a Gram matrix.\n\nIn summary, this thesis introduces techniques based on spherical neurons that enhance the GDL framework, with a specific focus on equivariant and invariant learning on point sets.
Sep 27, 2024
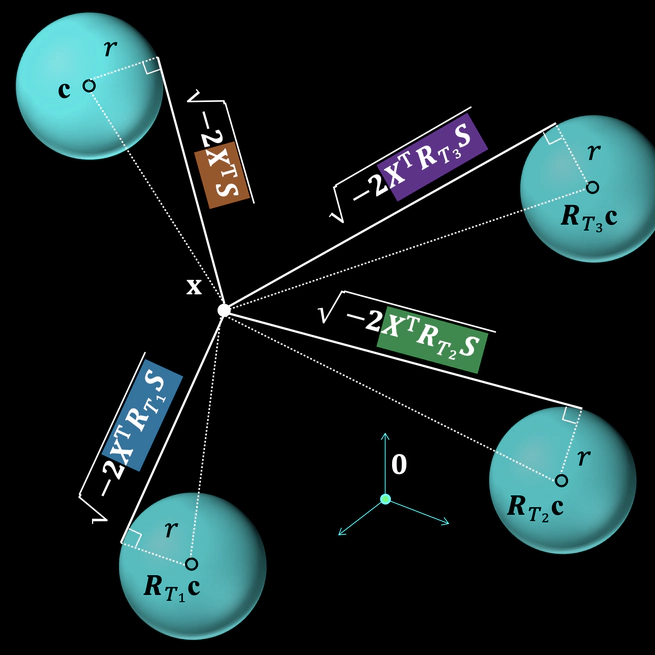
In this paper, we utilize hyperspheres and regular $n$-simplexes and propose an approach to learning deep features equivariant under the transformations of $n$D reflections and rotations, encompassed by the powerful group of $\text{O}(n)$. Namely, we propose $\text{O}(n)$-equivariant neurons with spherical decision surfaces that generalize to any dimension $n$, which we call Deep Equivariant Hyperspheres. We demonstrate how to combine them in a network that directly operates on the basis of the input points and propose an invariant operator based on the relation between two points and a sphere, which as we show, turns out to be a Gram matrix. Using synthetic and real-world data in $n$D, we experimentally verify our theoretical contributions and find that our approach is superior to the competing methods for $\text{O}(n)$-equivariant benchmark datasets (classification and regression), demonstrating a favorable speed/performance trade-off.
Jul 22, 2024
In many practical applications 3D point cloud analysis requires rotation invariance. In this paper we present a learnable descriptor invariant under 3D rotations and reflections i.e. the O(3) actions utilizing the recently introduced steerable 3D spherical neurons and vector neurons. Specifically we propose an embedding of the 3D spherical neurons into 4D vector neurons which leverages end-to-end training of the model. In our approach we perform TetraTransform—an equivariant embedding of the 3D input into 4D constructed from the steerable neurons—and extract deeper O(3)-equivariant features using vector neurons. This integration of the TetraTransform into the VN-DGCNN framework termed TetraSphere negligibly increases the number of parameters by less than 0.0002%. TetraSphere sets a new state-of-the-art performance classifying randomly rotated real-world object scans of the challenging subsets of ScanObjectNN. Additionally TetraSphere outperforms all equivariant methods on randomly rotated synthetic data: classifying objects from ModelNet40 and segmenting parts of the ShapeNet shapes. Thus our results reveal the practical value of steerable 3D spherical neurons for learning in 3D Euclidean space.
Jun 17, 2024
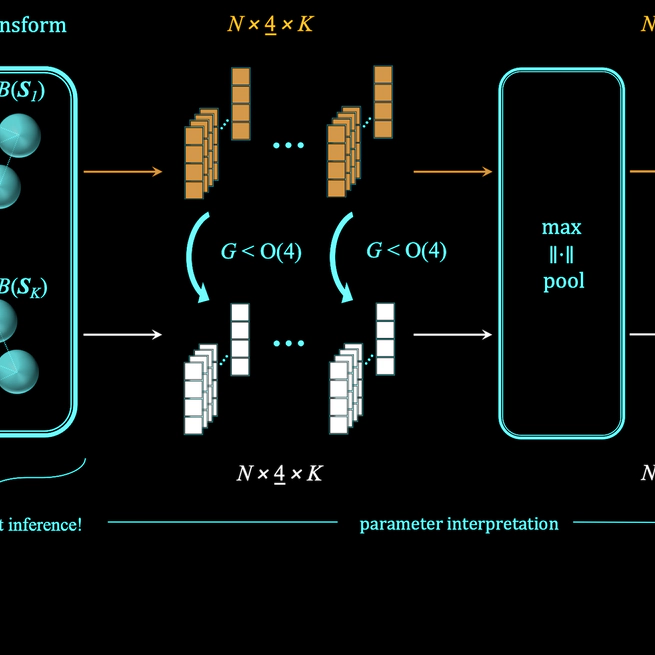
Emerging from low-level vision theory, steerable filters found their counterpart in prior work on steerable convolutional neural networks equivariant to rigid transformations. In our work, we propose a steerable feed-forward learning-based approach that consists of neurons with spherical decision surfaces and operates on point clouds. Such spherical neurons are obtained by conformal embedding of Euclidean space and have recently been revisited in the context of learning representations of point sets. Focusing on 3D geometry, we exploit the isometry property of spherical neurons and derive a 3D steerability constraint. After training spherical neurons to classify point clouds in a canonical orientation, we use a tetrahedron basis to quadruplicate the neurons and construct rotation-equivariant spherical filter banks. We then apply the derived constraint to interpolate the filter bank outputs and, thus, obtain a rotation-invariant network. Finally, we use a synthetic point set and real-world 3D skeleton data to verify our theoretical findings.
Jul 19, 2022