TetraSphere: A Neural Descriptor for O(3)-Invariant Point Cloud Analysis

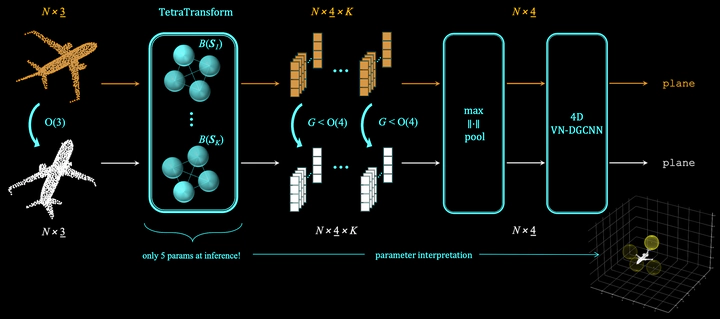
In many practical applications 3D point cloud analysis requires rotation invariance. In this paper we present a learnable descriptor invariant under 3D rotations and reflections i.e. the O(3) actions utilizing the recently introduced steerable 3D spherical neurons and vector neurons. Specifically we propose an embedding of the 3D spherical neurons into 4D vector neurons which leverages end-to-end training of the model. In our approach we perform TetraTransform—an equivariant embedding of the 3D input into 4D constructed from the steerable neurons—and extract deeper O(3)-equivariant features using vector neurons. This integration of the TetraTransform into the VN-DGCNN framework termed TetraSphere negligibly increases the number of parameters by less than 0.0002%. TetraSphere sets a new state-of-the-art performance classifying randomly rotated real-world object scans of the challenging subsets of ScanObjectNN. Additionally TetraSphere outperforms all equivariant methods on randomly rotated synthetic data: classifying objects from ModelNet40 and segmenting parts of the ShapeNet shapes. Thus our results reveal the practical value of steerable 3D spherical neurons for learning in 3D Euclidean space.