O$n$ Learning Deep O$(n)$ Equivariant Hyperspheres
Jul 22, 2024·
 ,
,
,
,
·
1 min read
,
,
,
,
·
1 min read
Pavlo Melnyk
Michael Felsberg
Mårten Wadenbäck
Andreas Robinson
Cuong Le
Abstract
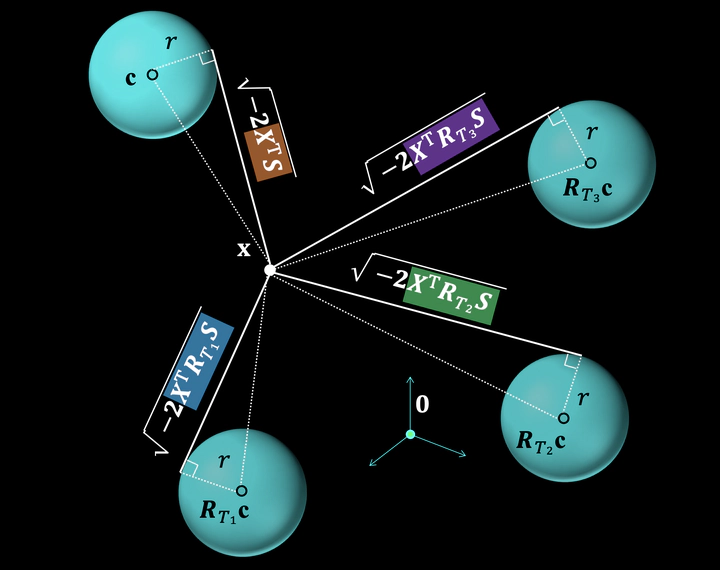
In this paper, we utilize hyperspheres and regular $n$-simplexes and propose an approach to learning deep features equivariant under the transformations of $n$D reflections and rotations, encompassed by the powerful group of $\text{O}(n)$. Namely, we propose $\text{O}(n)$-equivariant neurons with spherical decision surfaces that generalize to any dimension $n$, which we call Deep Equivariant Hyperspheres. We demonstrate how to combine them in a network that directly operates on the basis of the input points and propose an invariant operator based on the relation between two points and a sphere, which as we show, turns out to be a Gram matrix. Using synthetic and real-world data in $n$D, we experimentally verify our theoretical contributions and find that our approach is superior to the competing methods for $\text{O}(n)$-equivariant benchmark datasets (classification and regression), demonstrating a favorable speed/performance trade-off.
Type
Publication
In Proceedings of the 41st International Conference on Machine Learning